MAGNETIZING (NO-LOAD) CURRENT
Consider the simple pulse transformer circuit of Figure 2A and its equivalent circuit of Figure 2B.

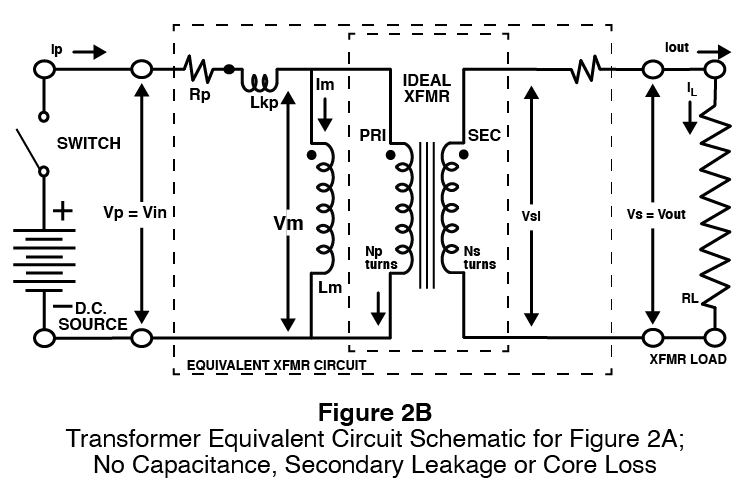
There is no source impedance, winding capacitances, or secondary leakage inductance to worry about. With both switches open, there cannot be any primary or secondary currents flowing. Now close the primary switch. Since the secondary load is not connected, the pulse transformer’s primary winding acts like an inductor placed across a voltage source. Primary current begins to flow. This is the magnetizing current (no secondary current) and is governed by the differential equation V(t) = L x d(I)/dt + Rp x I(t), with units of volts, henries, amps, and seconds. If the power supply has constant voltage, Rp = zero, & L = Lkp+Lm is constant, the differential equation can be solved for I(t), I(t) = Io + V x t / (Lkp+Lm), where Io = the initial current which equals zero. Notice that the current increases at a linear rate over time and that the rate in inversely proportional to the inductance. The current flows through Np turns creating Np x I(t) amount of magnetizing force (amp-turns) which in turns creates a magnetic flux density in the pulse transformer core. Eventually the increasing primary magnetizing current would exceed the magnetic flux capacity of the pulse transformer core and will saturate the core. Once saturation occurs the primary current rapidly increases towards infinity (in theory). In a real circuit the primary winding resistance (and source impedance) would limit the current. See Figure 3A below for graphical illustration. For non-zero Rp, I(t) = Io + (V/Rp) x e(-Rp x t / (Lkp + Lm)). The effect of Rp is graphically illustrated in Figures 3B and 3C. Rp extends the time it takes for the unloaded transformer (or an inductor) to saturate. If Rp is sufficiently large, it prevents the transformer (or inductor) from saturating altogether. Regardless of saturation, Rp places an upper limit on the primary current value.



Quick Menu
Questions or Concerns?
